The extension is called Burn-My-Windows and I always look forward to it when booting into GNOME because it feels so ✨fancy✨
VegOwOtenks
I stumbled over Gradience just yesterday but I tought it was archived sometime last year, is it still working accordingly?
Unfortunately not :/ But I do have rainbow-gradient window borders.
I suppose you're mainly concerned about LibAdwaita-Apps?
I was surprised to learn that
- a) macOS only recently added Left/Right-tiling natively (without extensions, just like GNOME does)
- b) they leave gaps when you tile them so that it looks like you messed up the tiling somehow
Thank you for the detailed answer, especially the explanation 'in more words' and the link helped me understand what happens in this Monoid instance.
Not the first year I participate but the first year I finished, 2021 was my all-time high so far with 42 stars when I was just starting oit and learning python. Knowing that there were more people in the same boat and that there was a competition kept me going, although the competiton also induced a lot of stress, not sure whether I want to keep the competitive attitude.
Thanks to everyone for uploding solutions, Ideas and program stats, this kept me optimizing away, which was a lot of fun!
I alwqys assumed you were Cameron Wu, who is?
Haskell
Have a nice christmas if you're still celebrating today, otherwise hope you had a nice evening yesterday.
import Control.Arrow
import Control.Monad (join)
import Data.Bifunctor (bimap)
import qualified Data.List as List
heights = List.transpose
>>> List.map (pred . List.length . List.takeWhile (== '#'))
parse = lines
>>> init
>>> List.groupBy (curry (snd >>> (/= "")))
>>> List.map (List.filter (/= ""))
>>> List.partition ((== "#####") . head)
>>> second (List.map List.reverse)
>>> join bimap (List.map heights)
cartesianProduct xs ys = [(x, y) | x <- xs, y <- ys]
part1 = uncurry cartesianProduct
>>> List.map (uncurry (List.zipWith (+)))
>>> List.filter (List.all (<6))
>>> List.length
part2 = const 0
main = getContents
>>= print
. (part1 &&& part2)
. parse
Thank you for showing this trick, I knew Haskell was lazy but this one blew my mind again.
Haskell
Part 1 was trivial, just apply the operations and delay certain ones until you have all the inputs you need.
Code
import Control.Arrow
import Data.Bits
import Numeric
import qualified Data.Char as Char
import qualified Data.List as List
import qualified Data.Map as Map
parse s = (Map.fromList inputs, equations)
where
ls = lines s
inputs = map (take 3 &&& (== "1") . drop 5) . takeWhile (/= "") $ ls
equations = map words . filter (/= "") . tail . dropWhile (/= "") $ ls
operations = Map.fromList
[ ("AND", (&&))
, ("XOR", xor)
, ("OR", (||))
]
solveEquations is [] = is
solveEquations is (e:es)
| is Map.!? input1 == Nothing = solveEquations is (es ++ [e])
| is Map.!? input2 == Nothing = solveEquations is (es ++ [e])
| otherwise = solveEquations (Map.insert output (opfunc value1 value2) is) es
where
value1 = is Map.! input1
value2 = is Map.! input2
opfunc = operations Map.! operation
(input1:operation:input2:_:output:[]) = e
wireNumber prefix = List.filter ((prefix `List.isPrefixOf`) . fst)
>>> flip zip [0..]
>>> List.filter (snd . fst)
>>> List.map ((2 ^ ). snd)
>>> sum
part1 = uncurry solveEquations
>>> Map.toList
>>> wireNumber "z"
part2 (is, es) = List.intercalate "," . List.sort . words $ "z08 ffj dwp kfm z22 gjh jdr z31"
main = getContents
>>= print
. (part1 &&& part2)
. parse
For part 2 I tried symbolic solving to detect discrepancies but I wouldn't achieve anything with it.
SymbolicEquation
data SymbolicEquation = Single { eqName :: String }
| Combine
{ eqName :: String
, eqOperation :: String
, eqLeft :: SymbolicEquation
, eqRight :: SymbolicEquation
}
deriving (Eq)
instance Show SymbolicEquation where
show (Single name) = name
show (Combine name op l r) = "(" ++ name ++ "= " ++ show l ++ " " ++ op ++ " " ++ show r ++ ")"
symbolicSolve is [] = is
symbolicSolve is (e:es)
| is Map.!? input1 == Nothing = symbolicSolve is (es ++ [e])
| is Map.!? input2 == Nothing = symbolicSolve is (es ++ [e])
| otherwise = symbolicSolve (Map.insert output (Combine output operation value1 value2) is) es
where
value1 = is Map.! input1
value2 = is Map.! input2
(input1:operation:input2:_:output:[]) = e
My solution was to use the dotEngine-function to translate the operations into a digraph in graphviz-style which I simply plotted and searched through using a python script.
dotEngine
dotEngine (input1:operation:input2:_:output:[]) = [
input1 ++ " -> " ++ output ++ " [ label=" ++ operation ++ "];"
, input2 ++ " -> " ++ output ++ " [ label=" ++ operation ++ "];"
]
I took a loook at the initial graph which was a vertical line with a few exception which I figured would be the misordered wires.
I did try some hardware-simulations in the far past to build bit-adders which helped me recognize patterns like carry calculation.
First I replaced all occurences of x__ XOR y__ -> w with x__ XOR y__ -> xor__ to recognize them more easily. The same with AND of xs and ys.
Using the following script I would then use some Regex to search for the rules that corresponded to carry calculations or structures I knew. The script would break exactly four times and I would then figure out what to switch by hand through looking at the updated graphViz.
Please excuse the bad coding style in the script, I had written it on the ipython-REPL.
python script
r = open("input").read()
for i in range(2, 45):
prevI = str(i - 1).zfill(2)
I = str(i).zfill(2)
forward = f"xor{I} AND carry{prevI} -> (\\w+)"
backward = f"carry{prevI} AND xor{I} -> (\\w+)"
m1 = re.search(forward, r)
m2 = re.search(backward, r)
if m1 is None and m2 is None:
print(forward, backward)
break
m = m1 or m2
r = r.replace(m.group(1), f"combinedCarry{I}")
forward = f"and{I} OR combinedCarry{I} -> (\\w+)"
backward = f"combinedCarry{I} OR and{I} -> (\\w+)"
m1 = re.search(forward, r)
m2 = re.search(backward, r)
if m1 is None and m2 is None:
print(forward, backward)
break
m = m1 or m2
r = r.replace(m.group(1), f"carry{I}")
open("input", "w").write()
When solving such a swapped wire problem I would then use my haskell function to plot it out again and stare at it for a few minutes until I understood wich parts belonged where.
The last one looked like this
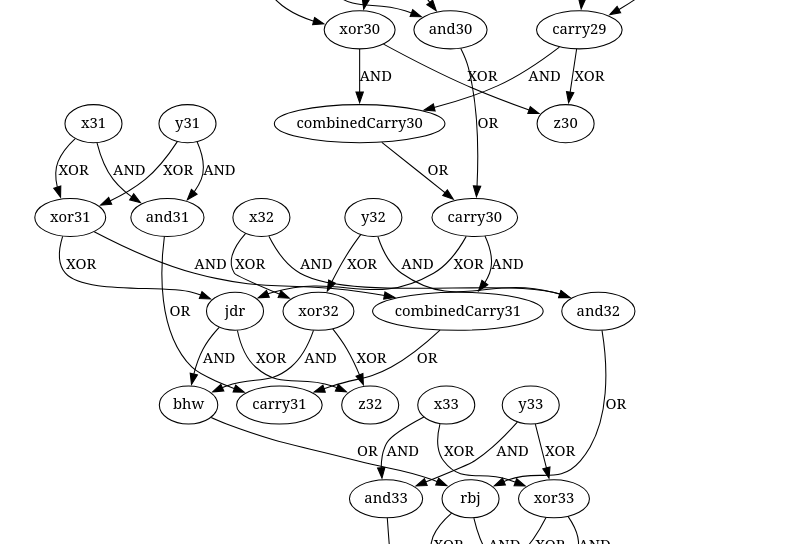
In this one I needed to switch jdr and carry31 to make it work.







I also like watching Doctor Who, how did you manage to make a cute dalek? :d