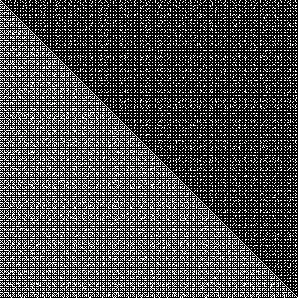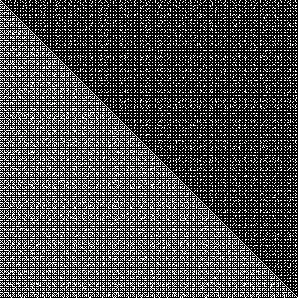The turtle follows the path of the Hilbert curve of some order < 10. What cool generative art could be generated by Hilbert curves besides walking through rgb-colors with it? I thought about generating 2D perlin-like-noise from 1D perlin-noise with it.

Procedurally generated video of stars and clouds moving using a parallax effect.

This video actually consists of multiple pieces of procedurally generated art combined together. These individual parts are the star and cloud textures, the code that animates them and the Bézier curve gradients that add colour.

I created this art as a part of Spaceships, a free/libre video game that I created. The game and this art are created in the Rust programming language and using the glium crate for rendering the video (this is a safe abstraction to OpenGL).

Each individual star texture is generated from four glowing lines that intersect the centre of the texture. I was inspired by GIMP's sparkle plugin on individual pixels when making this.

The clouds are generated using Perlin noise in a similar way to how this article generates them. The video uses three cloud images layered on top of each other.

The larger game that this is part of is 2D, but the sky background is 3D, with each individual star and cloud image having a z coordinate that gives a parallax effect when the camera moves.

What I have described so far would only generate a greyscale video. For the clouds, what adds colour are two Bézier curve gradients. Each of the two colour channels in each cloud image is treated as input to the Bézier curve which outputs an RGB colour. Once the clouds are rendered, the stars are rendered on top and coloured based on the colour of the generated clouds right under it.

Here are the source files that are used to generate this video. These only provide a partial picture as they depend on many other source files, but if you want to get an understanding of how the code works, these are a good place to start exploring.

1. Star texture generation code: https://codeberg.org/rustydev/spaceships/src/tag/v1.3.1/assets/src/textures/stars.rs
2. Cloud texture generation code: https://codeberg.org/rustydev/spaceships/src/tag/v1.3.1/assets/src/textures/clouds.rs
3. Animation: https://codeberg.org/rustydev/spaceships/src/tag/v1.3.1/src/playing/view/decorations/sky.rs
4. Gradient: https://codeberg.org/rustydev/spaceships/src/tag/v1.3.1/src/game/config.rs#L113-L119

We call two numbers x,y coprime if their greatest common divisor is 1.

Examples

• 9 and 8 are coprime
• 3 and 7 are coprime. gcd(3, 7) = 1
• 11 and 99 are not coprime, since gcd(99,11) = 11 != 1

Lower Diagonal y>x

A pixel x,y is marked black, if x and y are coprime.

Upper Diagonal x>y

A pixel x,y is marked black, if 2x+1 and 2y+1 are coprime

The different behavior for the upper/lower diagonal was chosen, since gcd is commotative, and the result would have been a boring mirror image.

generated with the following c-code:

#include "intmaths.h"
#include <stdio.h>
#include <assert.h>

int main(void){
  // tests to check if gcd works
  assert(3 == gcd(3*5, 3*7));
  assert(11 == gcd(11*5, 11*7));
  assert(1 == is_prime(3));
  int t1 = gcd(11*3*3, 3*7);
  assert(t1 == 3);
  int t2 = gcd(11*4, 4*7);
  assert(t2 == 4);
  int W = 300;
  int H = 300;
  int START = 2;
  printf("P1\n%d %d\n", W-START, H-START);
  for(int y=START; y<H; y++){
    for(int x=START; x<W; x++){
      int r2 = 0;
      if(x > y){
        // upper diagonal
        int xmod = 2*x+1;
        int ymod = 2*y+1;
        int gc = gcd(xmod, ymod);
        if(gc == 1){
          r2 = 1;
        }// pixel is marked black, if xmod and ymod are coprime, and we are in upper diagonal
      }else{
        int gc = gcd(x, y);
        if(gc == 1){
          r2 = 1;
        }
      }
      // int r2 = r % 2;
      printf("%d", r2);
    }
    printf("\n");
  }
  return 0;
}

gcd was calcualted using euclids algorithm.

Today we want to generate this star like shape using sums of trigeometric functions sin and cos:

Function:

f(x) = x/57 + x**3/19 

where x**3 is x^3 = x*x*x written in python

To calculate the x and y coordinate of the nth. step:

sx(n) = sum((75*cos(2*pi*f(i)) for i in range(n)))
sy(n) = sum((75*sin(2*pi*f(i)) for i in range(n)))

To render this with pythons turtle library, the following code can be used.

from math import cos, sin, pi, tan
def f(x):
    form = x/57 + x**3/19
    return form

def seq(fu):
    r = 75 # "zoom" level, kinda arbitrary choice so you can see it well
    s = [0, 0]
    for i in range(10000):
        s[0] += r*cos(2*pi*fu(i))
        s[1] += r*sin(2*pi*fu(i))
        yield s

import turtle
from time import sleep
for i in seq(f):
    turtle.setpos(i[0], i[1])
sleep(20)

This exponential sum with function f seems to have a limited convergence-radius / the sum stays in a bounded circle for longer than 10000 steps in my experiments. Can you proof this?

Further reading:

• https://en.wikipedia.org/wiki/Exponential_sum
• https://anvaka.github.io/e-sum/?code=x%2F57+%2B+xxx%2F19&bufferSize=12000&totalSteps=12000&spi=500

• Rule 90 in a square 100x100 image with a pseudorandom starting seed
• first saved as a .pbm file I later converted to .webp using an image viewer application
• I generated it with the following rust code …

use std::io::Write;

const WIDTH: usize = 100;
const HEIGHT: usize = 100;
type BITMAP = [[bool; WIDTH]; HEIGHT];
fn write_bitmap_file(filename: &str, bitmap: BITMAP) -> std::io::Result<()> {
    let mut file: std::fs::File = std::fs::File::create(filename)?;
    file.write_all(b"P1\n")?;
    file.write_all(format!("{} {}\n", WIDTH, HEIGHT).as_bytes())?;
    for y in 0..HEIGHT {
        let mut one_row = String::with_capacity(WIDTH + 1);
        for x in 0..WIDTH {
            if bitmap[y][x] {
                // one_row = format!("{}1", one_row);
                one_row.push('1');
            } else {
                one_row.push('0');
            }
        }
        one_row.push('\n');
        file.write_all(one_row.as_bytes())?;
    }
    Ok(())
}

fn applyrule(rulenr: u32, bitmap: &mut BITMAP) {
    for y in 1..HEIGHT {
        for x in 0..WIDTH {
            let mut rule_select = 0;
            for xpm in 0..3 {
                let addx = xpm as i32 - 1; // -1 to 1
                let idx: i32 = x as i32 + addx;
                if idx < 0 || idx == WIDTH as i32 {
                    continue;
                }
                let idx: usize = idx as usize;
                let reading = bitmap[y - 1][idx];
                if reading {
                    rule_select |= 1 << xpm;
                }
            }
            let rule_index = 1 << rule_select;
            if rulenr & rule_index != 0 {
                bitmap[y][x] = true;
            } else {
                bitmap[y][x] = false;
            }
        }
    }
}

fn main() {
    let randomseed: u128 = 0x46f470db4dbf5ac29b6e572f51ecafe;
    let mut bitmap: BITMAP = [[false; WIDTH]; HEIGHT];
    // populate first row width random values
    for x in 0..WIDTH {
        let xmod = x % 128;
        let curr = randomseed & (1 << xmod) == 0;
        bitmap[0][x] = curr;
    }
    applyrule(90, &mut bitmap);
    write_bitmap_file("rule90.bpm", bitmap).unwrap();
}

Fractals covered:

• Mandelbrot
• Koch-Curve
• …

Video description:

A prototype of the project of virtual breeding of digital plants by crossing. Each plant has a genome, which is an array of numbers. By crossing plants (mixing their genome), we get a new kind of plant. In this way, you can get very interesting and unusual results.

Summary generated by claude.ai from the video transcript:

A generative art project to create abstract images of imaginary plants. The creator starts with a genome represented as a sequence of numbers that gets fed into an algorithm to generate plant images. By evolving the genomes through processes like mutation and crossover, new plant images emerge. The creator discusses the challenges of defining an objective fitness function, since beauty is subjective. Without a fitness function for natural selection, the creator resorts to artificial selection by manually choosing genomes to crossover. The resulting plants have unique, imaginary qualities that can't be precisely predicted in advance. The creator notes some possible rules to make the plants more unique, like limiting how similar parent genomes can be. Overall, the project aims to explore an abstract generative space of imaginary plants through evolutionary techniques.

Generative art inspired by works of Loek Vugs. You can generate more variations and explore the code on this Observable notebook.